Chapter 3: Layer Models

Exercise 2

A Two-Layer Model. Insert another atmospheric layer into the model, just like the first one. The layer is transparent to visible light but a blackbody for infrared.

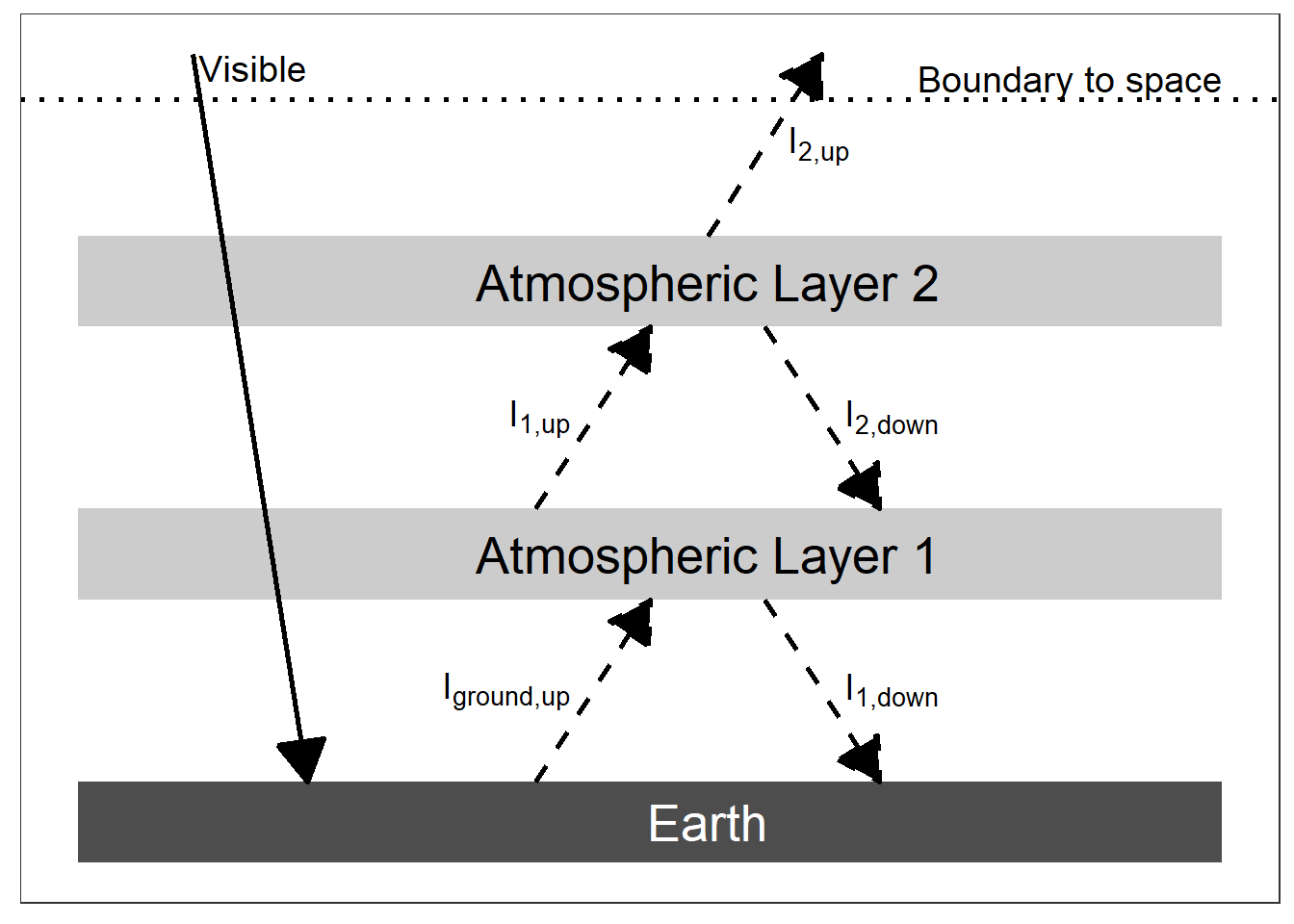
(#fig:two_layer_figure)An energy diagram for a planet with two panes of glass for an atmosphere. The intensity of absorbed visible light is \((1 - \alpha) I_{solar} / 4\).

1. Write the energy budgets for both atmospheric layers, for the ground, and for the Earth as a whole, like we did for the One-Layer Model.

Answer:

At each layer, calculate the heat in (in the diagram, this is the sum of all the intensities with arrows that end at the atmospheric layer) and the heat out (the sum of all the intensities that start at the atmospheric layer and have arrows pointing away from it).

• Top of the atmosphere: \(I_{2,\text{up}} = I_{\text{visible}} = (1 - \alpha) I_{\text{solar}} / 4\)
• Layer 2: \(I_{1,\text{up}} = I_{2,\text{up}} + I_{2,\text{down}}\)
• Layer 1: \(I_{\text{ground,up}} + I_{2,\text{down}} = I_{1,\text{up}} + I_{1,\text{down}}\)
• Ground: \(I_{\text{ground,up}} = I_{\text{visible}} + I_{1,\text{down}}\)

2. Manipulate the budget for the Earth as a whole to obtain the temperature T₂ of the top atmospheric layer, labeled Atmospheric Layer 2 in the figure above. Does this part of the exercise seem familiar in any way? Does the term ring any bells?

Top of the atmosphere:

\[ \begin{aligned} I_{2,\text{up}} &= I_{\text{visible}} = \frac{(1 - \alpha) I_{\text{solar}}}{4}\\ I_{2,\text{up}} &= \varepsilon \sigma T_2^4\\ T_2 &= \sqrt[4]{\frac{I_{2,\text{up}}}{\varepsilon \sigma}} \\ &= \sqrt[4]{\frac{(1 - \alpha) I_{\text{solar}}}{4 \varepsilon \sigma}} \\ &= T_{\text{bare rock}} \end{aligned} \]

This is the same as the bare-rock temperature.

Answer: The temperature of layer 2 is 254. K, which is the same as the bare-rock temperature. In layer models, the top layer of the atmosphere is always the bare-rock temperature.

3. Insert the value you found for T₂ into the energy budget for layer 2, and solve for the temperature of layer 1 in terms of layer 2. How much bigger is T₁ than T₂?

From the energy budget for Layer 2, I_1,up = I_2,up + I_2,down. The temperature of the bottom of the layer is the same as the temperature for the top of the layer, so I_2,down = I_2,up

\[ \begin{aligned} I_{\text{2,down}} &= I_{\text{2,up}} \\ I_{\text{1,up}} &= I_{\text{2,up}} + I_{\text{2,down}} \\ &= 2 I_{\text{2,up}} \\ T_1 &= \sqrt[4]{\frac{I_{\text{1,up}}}{\epsilon \sigma}} \\ &= \sqrt[4]{\frac{2 I_{\text{2,up}}}{\epsilon \sigma}} \\ &= \sqrt[4]{2} T_2 \\ &= \sqrt[4]{2}\; T_{\text{bare rock}} \\ \end{aligned} \]

Answer: The temperature of layer 1 is 302. K. This is the same as the ground temperature in a 1-layer model.

4. Now insert the value you found for T₁ into the budget for atmospheric layer 1 to obtain the temperature of the ground, T_ground. Is the greenhouse effect stronger or weaker because of the second layer?

From the energy budget for layer 1,

\[ \begin{aligned} I_{\text{ground,up}} + I_{\text{2,down}} &= I_{\text{1,up}} + I_{\text{1,down}} \\ I_{\text{ground,up}} &= I_{\text{1,up}} + I_{\text{1,down}} - I_{\text{2,down}} \\ \text{we} &\text{ know that} \\ I_{\text{1,down}} &= I_{\text{1,up}} \\ &\text{and} \\ I_{\text{2,down}} &= I_{\text{2,up}} \\ &\text{so} \\ I_{\text{ground,up}} &= 2 I_{\text{1,up}} - I_{\text{2,up}} \\ \text{we} &\text{ also know that} \\ I_{\text{1,up}} &= 2 I_{\text{2,up}} \\ &\text{so} \\ I_{\text{ground,up}} &= 4 I_{\text{2,up}} - I_{\text{2,up}} \\ &= 3 I_{\text{2,up}} \end{aligned} \]

\[ \begin{aligned} T_{\text{ground}} &= \sqrt[4]{\frac{I_{\text{ground,up}}}{\varepsilon \sigma}} \\ &= \sqrt[4]{\frac{3 I_{\text{2,up}}}{\varepsilon \sigma}} \\ &= \sqrt[4]{3}\; T_2 \\ &= \sqrt[4]{3}\; T_{\text{bare rock}} \end{aligned} \]

Answer: T_ground = 334. K = \(\displaystyle\sqrt[4]{3 T_{\text{bare rock}}}\)

In a 1-layer model, the ground temperature was \(\sqrt[4]{2}\) times the bare-rock temperature, and in a 2-layer model, the ground temperature is \(\sqrt[4]{3}\) times the bare-rock temperature.

Exercise 3

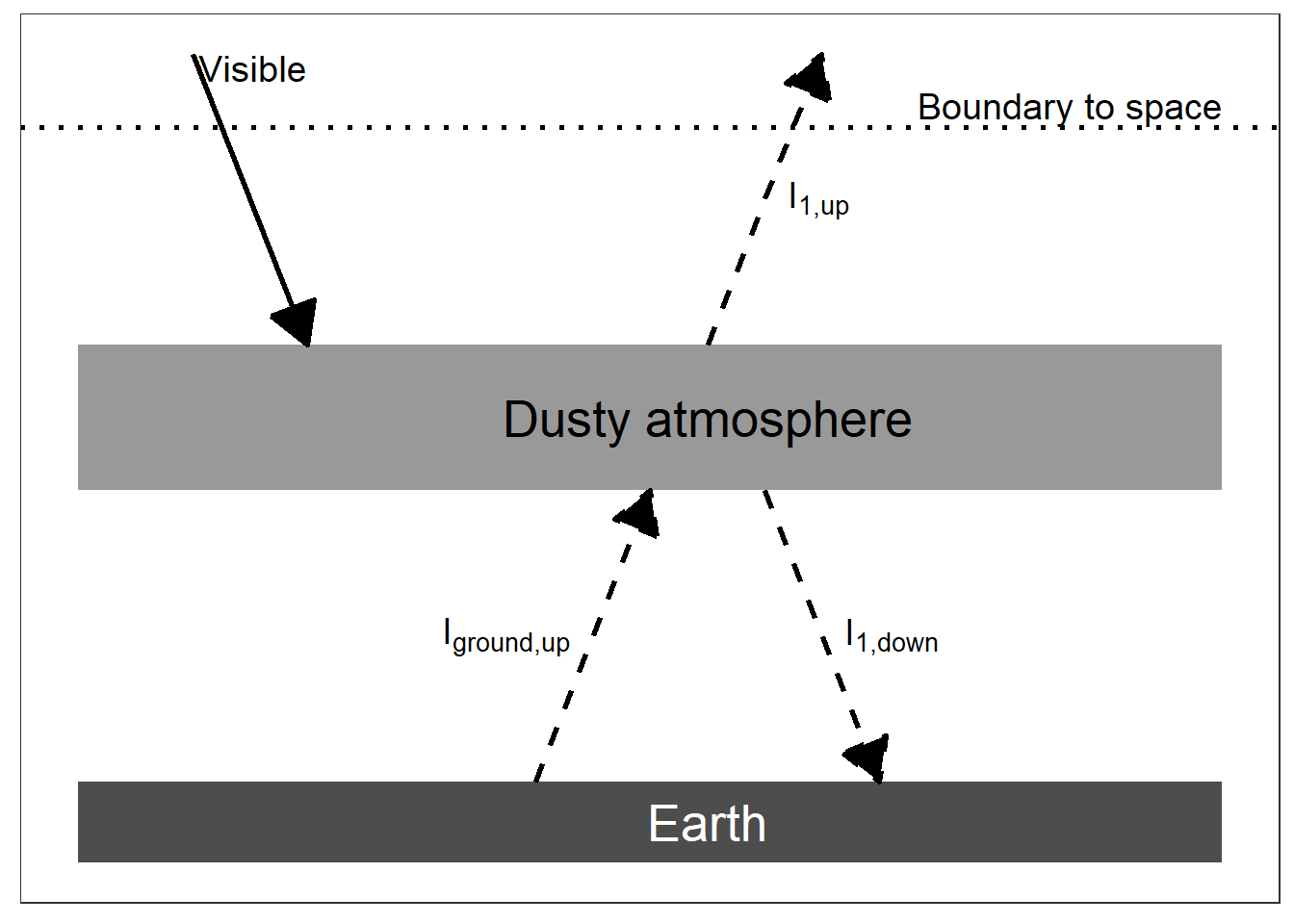
(#fig:nuclear_winter_diagram)An energy diagram for a planet with an opaque pane of glass for an atmosphere. The intensity of absorbed visible light is \((1 - \alpha) I_{solar} / 4\).

Nuclear Winter. Let us go back to the One-Layer Model but change it so that the atmospheric layer absorbs visible light rather than allowing it to pass through (See the figure above). This could happen if the upper atmosphere were filled with dust. For simplicity, assume that the albedo of the Earth remains the same, even though in the real world it might change with a dusty atmosphere.> What is the temperature of the ground in this case?

Answer: Here, the key difference is that the heat from the sun is absorbed by the atmosphere instead of passing through the atmosphere to the ground.

The equation for the atmosphere is the same as in the 1-layer model because we use the energy balance at the boundary to space:

\[I_{\text{atm, up}} = I_{\text{visible}} = \frac{(1 - \alpha) I_{\text{solar}}}{4}\]

and the temperature of the atmosphere is the bare-rock temperature, just as the top layer of the atmosphere is for every layer model.

However, things are different at the ground. The energy balance at the dusty atmosphere is

\[ \begin{aligned} I_{\text{visible}} + I_{\text{ground,up}} &= I_{\text{atm,up}} + I_{\text{atm,down}} \\ I_{\text{ground,up}} &= I_{\text{atm,up}} + I_{\text{atm,down}} - I_{\text{visible}} \\ & \text{But} \\ I_{\text{atm,up}} &= I_{\text{atm,down}} = I_{\text{visible}}. \\ & \text{So} \\ I_{\text{ground,up}} &= I_{\text{atm,up}}. \\ \text{This} & \text{ means that} \\ T_{\text{ground}} &= T_{\text{atmosphere}} = T_{\text{bare-rock}} \end{aligned} \]

T_ground = 254. K. This is the same as the bare-rock temperature.

The effect of the dust in the atmosphere is to cancel out the greenhouse effect and cool off the surface to the bare-rock temperature. The greenhouse effect works because the atmosphere is transparent to shortwave light and opaque to longwave light. If the atmosphere becomes opaque to shortwave light, then the greenhouse effect doesn’t work.